Don’t panic: It’s only the Simpson’s Paradox

Eventually, it catches you cold: Your results on the overall patient level contradict results on the subgroup level – leaving you in confusion or even despair.
However, there is no need to panic. With a deeper look into the data, one can get to the bottom of this observation.
Consider the following example: In a clinical trial, the dose-response relationship of a drug should be evaluated. Statistical analysis led to the following results:
| Dose-response correlation | Gender | Overall | |
|---|---|---|---|
| Female | Male | ||
| Pearson correlation coefficient r | -0.49 | -0.50 | 0.52 |
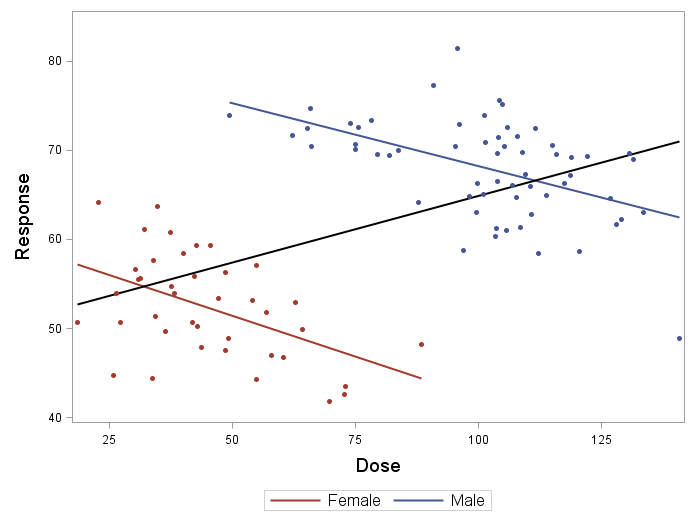
As expected, the results of the overall analysis population showed a positive dose-response effect (r = 0.52). That is, the higher the dose, the higher was the response. However, in a subgroup analysis of gender, the reverse association was found for each gender: The higher the dose, the lower was the response for both, female (r = -0.49) and male (r = -0.50).
What did happen here?
At the first sight, one might think, a rare curiosity may have arisen here. But this phenomenon is well known in science and called the Simpson’s Paradox.
The Simpson’s Paradox may arise if there is (at least) one confounding variable that has not been accounted for.
In our example, the factor gender influences the choice of drug dose as well as the response (as it is depicted in the figure below): Females took drugs with lower doses and were observed to respond less to the treatment compared to men. That is, the factor gender confounds the relationship between dose and response.
What can we do about it?
Non-adjusted results on the aggregated patient level simply do not convey the true and more complicated structure of the dose-response relationship in the population of interest. They are, hence, inadequate to be reported and lead to false conclusions.
Regression analyses techniques handle all kinds of confounding. Resulting association estimates (e.g. regression effects, odds ratios of logistic regression) are adjusted for confounding. This adjustment helps us to draw the right conclusions. In case of simple confounding structures with one or two confounding factors (like gender in our example), subgroup analyses (i.e. analyses conducted separately in subgroups) may be chosen.
In the current example, a regression model for response could be chosen – with dose as explanatory variable and gender as an additional confounding factor. The model estimation leads to appropriate negative correlation estimates (i.e. negative regression effects) for the dose-response relationship right away.
In summary, there is no need to despair when contradicting results on the aggregated population and subgroup level arise. However, it might be a challenging task to identify complicated confounding structures; A task that is most often accomplished in an interdisciplinary team of medical researchers and biostatisticians since the identification of confounding variables and techniques to handle them needs both, medical insight and statistical knowledge.
Picture: @Matthias Buehner /Fotolia.com









